Логические элементы и логические функции.
Элементы математической логики.
Логическая функция - это функция логических переменных, которая
может принимать только два значения : 0 или 1. В свою очередь,
сама логическая переменная (аргумент логической функции) тоже может
принимать только два значения : 0 или 1.
Логический элемент - это устройство, реализующее ту или иную
логическую функцию.
Y=f(X1,X2,X3,...,Xn) - логическая функция, она может быть задана
таблицей, которая называется таблицей истинности.
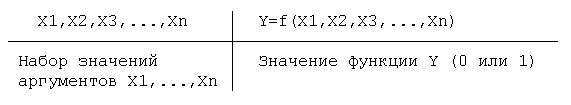
Число строк в таблице - это число возможных наборов значений
аргументов. Оно равно 2n, где n - число переменных.
Число различных функций n переменных равно 22^n.
Логические функции одной переменной
Таблица истинности функции одной переменной Y=f(X) содержит всего
2 строки, а число функций одной переменной равно 4.
1. Функция константа 0, Y=0. Техническая реализация этой функции -
соединение вывода Y с общей шиной с нулевым потенциалом.
Таблица истинности функции константа 0 имеет вид:
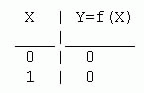
2. Функция Y=f(X)=X - функция повторения. Техническая реализация
этой функции - соединение между собой выводов X и Y.
Таблица истинности функции повторения имеет вид:
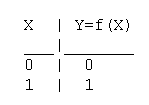
3. Функция Y=f(X)=NOT(X) - отрицание НЕ или инверсия (NOT(X) - это НЕ X).
Техническая реализация этой функции - инвертор на любом транзисторе
или логическом элементе, или транзисторный ключ.
Таблица истинности функции отрицания имеет вид:
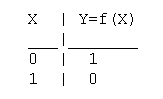
Логический элемент НЕ обозначается на схемах следующим образом:
(пишется X c чертой сверху)
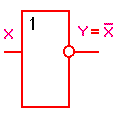
4. Функция константа 1, Y=1. Техническая реализация этой функции -
соединение вывода Y с источником питания.
Таблица истинности функции константа 1 имеет вид:
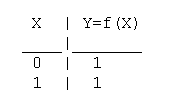
Важнейшей функцией одной переменной является отрицание НЕ,
остальные функции являются тривиальными.
Логические функции двух переменных
Таблица истинности функции двух переменных Y=f(X1,Х2) содержит 4
строки, а число функций двух переменных равно 16.
Мы рассмотрим только несколько основных функций двух переменных.
1. Логическое ИЛИ (логическое сложение, дизъюнкция):
Y= X1 + X2 = X1VX2
Техническая реализация этой функции - два параллельно соединенных
ключа:
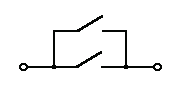
Таблица истинности логического ИЛИ имеет вид:
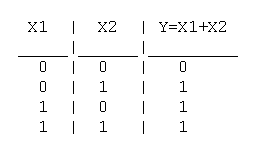
Логический элемент ИЛИ обозначается на схемах следующим образом:
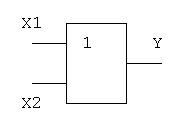
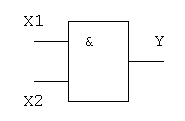
2. Логическое И (логическое умножение, конъюнкция, схема совпаде-
ний): Y = X1X2 = X1&X2
Техническая реализация этой функции - два последовательно сое-
диненных ключа:
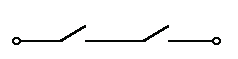
Таблица истинности логического И имеет вид:
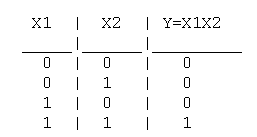
Логический элемент И обозначается на схемах следующим образом:
3. Функция стрелка Пирса (ИЛИ-НЕ): Y = NOT(X1+X2) Таблица истинности функции ИЛИ-НЕ имеет вид:
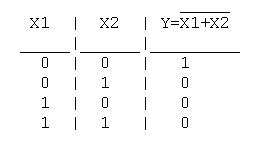
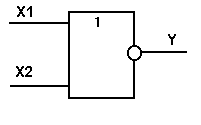
Логический элемент ИЛИ-НЕ обозначается на схемах следующим образом
:
4. Функция штрих Шеффера (И-НЕ): Y = X1|X2 = NOT(X1X2) Таблица истинности функции И-НЕ имеет вид:
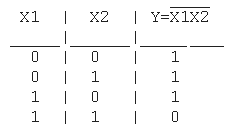
Логический элемент И-НЕ обозначается на схемах следующим образом:
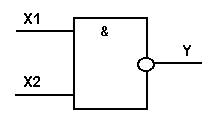
Есть ещё три логические функции двух переменных, имеющие специ-
альные названия: импликация, эквивалентность, неравнозначность
(исключающее ИЛИ, сложение по модулю 2). Последние две функции
являются взаимно обратными, также как, например, функция И и
функция штрих Шеффера.
Элемент памяти - RS-триггер
Триггер - это логическое устройство, способное хранить 1 бит ин-
формации. К триггерам относятся устойства, имеющие два устойчивых
состояния. Простейший триггер - RS-триггер, образован из двух
элементов И-НЕ (или ИЛИ-НЕ). Он позволяет запоминать 1 бит инфор-
мации, поскольку информация в компьютере представляется в двоич-
ном виде. Его схема приведена ниже.
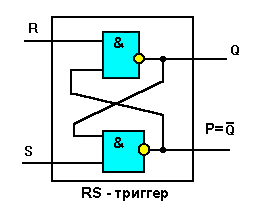
Действие RS-триггера поясняется в приведенной ниже таблице ис-
тинности. S-вход установки (Set), R-вход сброса (Reset).
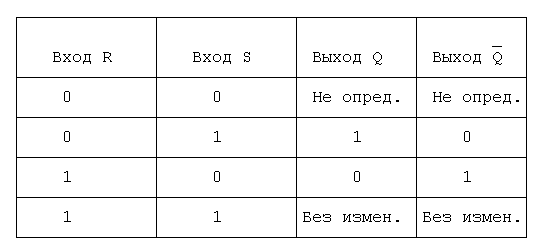
В обычном (исходном) состоянии на входы триггера поданы 1. Для записи информации на вход R подан 0. Для сброса информации и под- готовки к приёму новой информации на вход S подается 0 и триггер вернётся в исходное состояние. Поскольку один триггер запоминает 1 бит информации, то для запо- минания 1 байта (8 бит) нужно 8 триггеров, для запоминания 1 Кб (1024 байт) надо 8192 триггеров. Современные микросхемы ОЗУ спо- собны запоминать десятки мегабайт информации.
Элементы математической логики
Существуют такие наборы логических функций, с помощью которых
можно выразить любые другие логические функции. Они называются
функционально полными или базисами. Наиболее известный базис -
это набор функций И, ИЛИ, НЕ. Функция штрих Шеффера является ба-
зисной, также как и функция стрелка Пирса. Поэтому, с помощью ло-
гических элементов ИЛИ-НЕ или И-НЕ можно собрать любую логическую
схему. На таких элементах собран микропроцессор компьютера и дру-
гие логические устройства. Логические схемы состоят из логических
элементов, осуществляющих логические операции.
Логика - наука, изучающая методы установления истинности или лож-
ности одних высказываний на основе истинности или ложности других
высказываний (утверждений). Логика изучает методы доказательств и
опровержений. Логика составляет основу всякого управления, в том
числе технологическими процессами.
Математическая логика - современная форма логики, опирающаяся на
формальные математические методы.
Основные объекты логики - высказывания, то есть предложения, ко-
торые могут быть либо истинными, либо ложными. Существуют два
подхода установления истинности высказываний: эмпирический (опыт-
ный) и логический. При эмпирическом подходе истинность высказыва-
ний устанавливается на основе наблюдений, экспериментов, докумен-
тов и других фактов. При логическом подходе истинность высказыва-
ний доказывается на основе истинности других высказываний, то
есть чисто формально, на основе рассуждений без обращения к фак-
там.
В языках программирования QBasic и Turbo Pascal логические функ-
ции И, ИЛИ, НЕ реализуются в виде логических операций OR (ИЛИ),
AND (И), NOT (НЕ).
Множество всех логических функций, на котором определены три ло-
гические операции И, ИЛИ, НЕ называется булевой алгеброй (по име-
ни основоположника математической логики английского математика
Джорджа Буля). Упрощение формул в булевой алгебре производится на
основе эквивалентных преобразований, опирающихся на следующие ос-
новные законы (эквивалентные соотношения):

Кроме того, применяются ещё три соотношения:
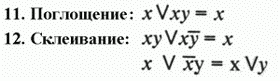
Законы 1,2,3,7 показывают, что свойства конъюнкции очень похожи на свойства умножения, поэтому её часто называют логическим умно- жением. Из законов 6 и 8 следует, что используя отрицание, дизъ- юнкцию можно выразить через конъюнкцию, и наоборот:
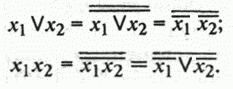
Это означает, что наборы И-НЕ и ИЛИ-НЕ также являются функцио- нально полными или базисными.
Вопросы
1. Что такое логическая функция и логический элемент?
2. Что такое таблица истинности и сколько в ней строк?
3. Какие функции одной переменной Вы знаете? Какая из них являет-
ся важнейшей?
4. Как зависит число функций от числа переменных?
5. Что такое конъюнкция и дизъюнкция? Как они реализуются?
6. Что такое функция стрелка Пирса? Какова её таблица истинности?
7. Что такое функция штрих Шеффера? Какова её таблица истинности?
8. Что такое базисная функция и какие базисы Вы знаете?
9. Что такое логика? Какие два подхода существуют в логике?
10. Как доказывается истинность или ложность высказываний? Приве-
дите примеры из практики.
11. Что такое булева алгебра?
12. Какие законы булевой алгебры Вы знаете? Где они применяются?
13. Что такое триггер? Как работает RS-триггер?
14. Сколько надо триггеров, чтобы запомнить 1 Мб информации?